fourier.html

Fourier-rækker

Jesper Libak Larsen

> restart:

> a[0]:=1/(2*L)*int(f(x),x=-L..L);

a[0] := 1/2*int(f(x), x = -L .. L)/L

> a[n]:=1/L*int(f(x)*cos(n*Pi*x/L),x=-L..L);

a[n] := int(f(x)*cos(n*Pi*x/L), x = -L .. L)/L

> b[n]:=1/L*int(f(x)*sin(n*Pi*x/L),x=-L..L);

b[n] := int(f(x)*sin(n*Pi*x/L), x = -L .. L)/L

> f1:=unapply(a[0]+sum(a[n]*cos(n*Pi*x/L)+b[n]*sin(n*Pi*x/L),n=1..ant),x,L,ant);

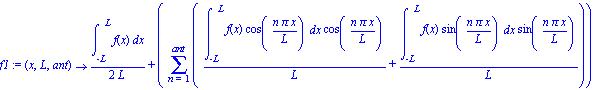
f1 := proc (x, L, ant) options operator, arrow; 1/2*int(f(x), x = -L .. L)/L+(sum(int(f(x)*cos(n*Pi*x/L), x = -L .. L)*cos(n*Pi*x/L)/L+int(f(x)*sin(n*Pi*x/L), x = -L .. L)*sin(n*Pi*x/L)/L, n = 1 .. an...

> f:=x->x;

> f1(x,2,5);

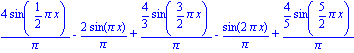
4*sin(1/2*Pi*x)/Pi-2*sin(Pi*x)/Pi+4/3*sin(3/2*Pi*x)/Pi-sin(2*Pi*x)/Pi+4/5*sin(5/2*Pi*x)/Pi

> plot([f(x),f1(x,2,5)],x=-5..5,y=-3..3,scaling=constrained,thickness=2);

[Plot]

> with(plots):

Warning, the name changecoords has been redefined

> animate( f1(x,2,ant),x=-5..5,ant=0..25,frames=50,numpoints=200,scaling=constrained,thickness=2);

[Plot]

> plot([int(f(x),x=0..2),int(f1(x,2,ant),x=0..2)],ant=0..15);

[Plot]

Ny funktion. Stykvis defineret, symmetrisk om x=0.

> restart:

> f(x)=piecewise(x<1,x,x>1,-x+2); plot(piecewise(x<1,x,x>1,-x+2),x=-1..3,scaling=constrained,thickness=2);

[Plot]

> a[0]:=1/(L)*(int(f[1](x),x=0..L/2)+int(f[2](x),x=L/2..L));

a[0] := (int(f[1](x), x = 0 .. 1/2*L)+int(f[2](x), x = 1/2*L .. L))/L

> a[n]:=2/L*(int(f[1](x)*cos(n*Pi*x/L),x=0..L/2)+int(f[2](x)*cos(n*Pi*x/L),x=L/2..L));

a[n] := 2*(int(f[1](x)*cos(n*Pi*x/L), x = 0 .. 1/2*L)+int(f[2](x)*cos(n*Pi*x/L), x = 1/2*L .. L))/L

> f1:=unapply(a[0]+sum(a[n]*cos(n*Pi*x/L),n=1..ant),x,L,ant);

f1 := proc (x, L, ant) options operator, arrow; (int(f[1](x), x = 0 .. 1/2*L)+int(f[2](x), x = 1/2*L .. L))/L+(sum(2*(int(f[1](x)*cos(n*Pi*x/L), x = 0 .. 1/2*L)+int(f[2](x)*cos(n*Pi*x/L), x = 1/2*L .....

> f[1]:=x->x;f[2]:=x->-x+2;

> f1(x,2,10);

> plot([f[1](x),f[2](x),f1(x,2,10)],x=-1..5,y=-1..1.5,scaling=constrained,thickness=2);

[Plot]

> with(plots):

Warning, the name changecoords has been redefined

> animate( f1(x,2,ant),x=-1..5,ant=0..20,frames=30,numpoints=200,scaling=constrained,thickness=2);

[Plot]

> plot(int(f1(x,2,ant),x=0..2),ant=0..3);

[Plot]

Samme funktion, symmetrisk om origo.

> restart:

> b[n]:=2/L*(int(f[1](x)*sin(n*Pi*x/L),x=0..L/2)+int(f[2](x)*sin(n*Pi*x/L),x=L/2..L));

b[n] := 2*(int(f[1](x)*sin(n*Pi*x/L), x = 0 .. 1/2*L)+int(f[2](x)*sin(n*Pi*x/L), x = 1/2*L .. L))/L

> f1:=unapply(sum(b[n]*sin(n*Pi*x/L),n=1..ant),x,L,ant);

f1 := proc (x, L, ant) options operator, arrow; sum(2*(int(f[1](x)*sin(n*Pi*x/L), x = 0 .. 1/2*L)+int(f[2](x)*sin(n*Pi*x/L), x = 1/2*L .. L))*sin(n*Pi*x/L)/L, n = 1 .. ant) end proc

> f[1]:=x->x;f[2]:=x->-x+2;

> f1(x,2,5);

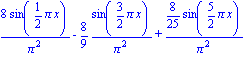
8*sin(1/2*Pi*x)/(Pi^2)-8/9*sin(3/2*Pi*x)/(Pi^2)+8/25*sin(5/2*Pi*x)/(Pi^2)

> plot([f[1](x),f[2](x),%],x=-2..8,y=-1..1.5,scaling=constrained,thickness=2);

[Plot]

> plot([int(f[1](x),x=0..1)+int(f[2](x),x=1..2),int(f1(x,2,ant),x=0..2)],ant=0..15,y=0.9..1.1);

[Plot]

Stykvis defineret funktion. Symmetrisk om x=0. Funktionen opstilles vha. Maples piecewise() funktion

> restart:

> a[0]:=1/L*int(f(x),x=0..L);

a[0] := int(f(x), x = 0 .. L)/L

> a[n]:=2/L*int(f(x)*cos(n*Pi*x/L),x=0..L);

a[n] := 2*int(f(x)*cos(n*Pi*x/L), x = 0 .. L)/L

> f1:=unapply(a[0]+sum(a[n]*cos(n*Pi*x/L),n=1..ant),x,L,ant);

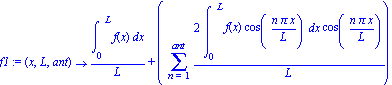
f1 := proc (x, L, ant) options operator, arrow; int(f(x), x = 0 .. L)/L+(sum(2*int(f(x)*cos(n*Pi*x/L), x = 0 .. L)*cos(n*Pi*x/L)/L, n = 1 .. ant)) end proc

> f(x):=piecewise(x<1,-exp(x)+2,x<2,x,x<3,7*x^2-35*x+44,x<4,1/2,x<5,sin(5*x-4),x<6,cos(x),x<7,-1,x<8,1,x<9,63/2*x^3-1611/2*x^2+6859*x-19448,x<10,-x+10);

f(x) := PIECEWISE([-exp(x)+2, x < 1], [x, x < 2], [7*x^2-35*x+44, x < 3], [1/2, x < 4], [sin(5*x-4), x < 5], [cos(x), x < 6], [-1, x < 7], [1, x < 8], [63/2*x^3-1611/2*x^2+6859*x-19448, x < 9], [-x+10...

> plot(f(x),x=0..10,scaling=constrained,thickness=2);

[Plot]

> plot([f(x),f1(x,10,20)],x=0..10,scaling=constrained,thickness=2,numpoints=100);

[Plot]

> plot([f(x),f1(x,10,80)],x=0..10,scaling=constrained,thickness=2,numpoints=100);

[Plot]