Løsning af differentialligninger ved hjælp af Maple.

Almindelige differentialligninger.

For at få størst mulig nytte af Maple i forbindelse med løsning af differentialligninger, skal pakken DEtools kaldes med with() .

> with(DEtools);

Tip: for at få Maple til at undlade at udskrive et resultat/ output (det med blåt), kan man afslutte kommandoen med kolon (:) i stedet for semikolon (;) , som normalt benyttes.

> with(DEtools):

Differentialoperatoren hedder i Maple diff() . Et differentiale indtastes altså på følgende måde: diff(udtryk,variable)

> diff(sin(x),x);

Eks. 1: 1. orden 1, grad, separable. Løs differentialligningen

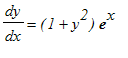
Den afhængige variable y skal i Maple indtastes som en funktion af den uafhængige variable x på følgende måde: y(x) .

> DL1 := diff(y(x),x) = (1+y(x)^2)*exp(x);

I pakken DEtools findes kommandoen odeadvisor . Kommandoen kategoriserer den pågældende differentialligning.

> odeadvisor(DL1);

dsolve() er den grundlæggende kommando til løsning af differentialligninger.

> L1 := dsolve(DL1);

_C1 er en arbitrær konstant.

Da Maple i yderst sjældne tilfælde regner forkert, er det en god ide, altid at kontrollere resultatet med kommandoen odetest , vises et 0 (nul) er resultatet korrekt.

Tip: For ikke at udskrive indholdet af variablen L1 til skærmen (som jo lige er blevet defineret), skrives i stedet 'L1' altså omgivet af apostrof.

> 'L1'; L1;

Tip: benyt [ ] til at angive indeks, f.eks. bliver y[p](t) til .

> test['L1'] = odetest(L1, DL1);

Resultatet kan også kontrolleres på følgende måde:

> subs(L1, DL1);

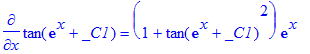
For at overskueliggøre dette, kan kommandoen Simplify benyttes. Procenttegnet henviser til det sidst udregnet resultat.

> simplify(%);

Umiddelbart kan det virke fjollet, at der i Maple findes en kommando til kontrol af et resultat som programmet selv er kommet med, for hvordan skulle programmet vide at dets egen løsning er forkert? Under løsningsprocessen, kaldes der automatisk andre kommandoer efter behov, en evt. fejl behøver således ikke nødvendigvis, at være opstået i kommandoen dsolve , men kan lige så godt være opstået i f.eks. integrationsprocessen. Nedenstående er et godt eksempel på vigtigheden af altid at benytte kommandoen odetest . NB: problemet kan være løst i en opdateret, eller nyere version af Maple.

> DiffLign:=diff(y(x),x)=sqrt(ln(x))/(x*sqrt(-1+x));

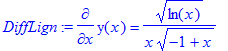
> Løsning:=dsolve(DiffLign);

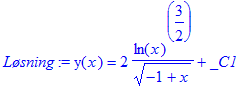
Nu skal resultatet så kontrolleres, og et 0 (nul) indikerer jo en korrekt løsning.

> odetest(Løsning,DiffLign);

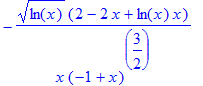
Som det fremgår, er løsningen ikke korrekt. Vi kan prøve at integrere udtrykket. rhs henviser til højre side af en ligning

> udtryk:=rhs(DiffLign);

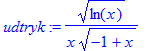
> INT:=int(udtryk,x);

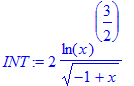
og derefter differentiere det igen

> DIFF:=diff(INT,x);

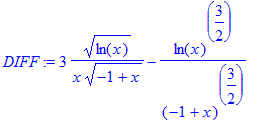
Nu skulle udtryk og DIFF have samme værdi for en hvilken som helst værdi af x.

Tip: benyt kommandoen evalb for at kontrollere om to udtryk er ens.

> evalb(udtryk=DIFF);

Det kan også kontrolleres grafisk.

> plot([udtryk,DIFF],x=0..5,y=0..5);

Eks. 2: 1. orden 1, grad, seprable. Find det partikulære integral til 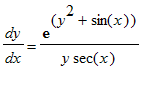der går gennem . Her skal der altså angives begyndelsesbetingelser.

Først skrives ligningen op.

> DL2 := diff(y(x),x) = (exp(y(x)^2+sin(x)))/(y(x)*sec(x));

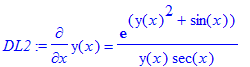
> odeadvisor(DL2);

Her i eksemplet, starter vi med at finde den fuldstændige løsning.

> L2 := dsolve(DL2, y(x));

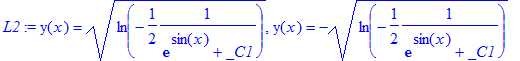
Da differentialligningen har to løsninger, skal begge testes. Løsningen deles op med [n] , idet n=1 angiver den første del af resultatet, og n = 2, den anden del.

> test['L2[1]'] = odetest(L2[1],DL2); test['L2[2]'] = odetest(L2[2],DL2);

I tilfælde med mange løsninger, bliver ovennævnte fremgangsmåde meget omstændelig, og der kan derfor med fordel anvendes en af følgende to testmetoder:

1) resultatet kan vises implicit ved at tilføje kommandoen implicit på følgende måde:

> L2:=dsolve(DL2, implicit);

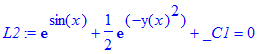
Som det ses her under, er dette resultat noget nemmere at teste.

> test['L2']=odetest(L2,DL2);

2) Er det ikke tilfredsstillende at have resultatet implicit, kan man benytte funktionen map. Med denne funktion opereres der med hvert element i en liste, i vores tilfælde testes hvert element.

> L2:=dsolve(DL2);

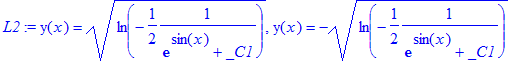
> test['L2'] = map(odetest,[L2],DL2);

Hvis alle elementerne i listen er 0 (nul) er de respektive resultater korrekte.

Da vi blev bedt om at bestemme den partikulære løsning til DL2, er det nødvendigt at angive begyndelsesbetingelser. Dette gøres på følgende måde:

> dsolve({DL2, y(0)=sqrt(ln(2))}, y(x));

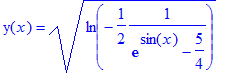
Eks. 3: 1 orden, 1 grad, homogen. Løs Differentialligningen 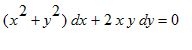, ligningen omskrives til

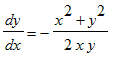
> DL3:=diff(y(x),x)=-(x^2+y(x)^2)/(2*x*y(x));

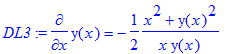
> odeadvisor(DL3);

> L3:=dsolve(DL3,implicit);

> test['L3']=odetest(L3,DL3);

Idet Maple før konstaterede, at DL3 havde form som en Bernoilli differentialligning, kan specialkommandoen bernoullisol anvendes. Derved løser Maple den hurtigere jf. nedenstående tip.

Tip: hvis man vil se hvilken fremgangsmåde Maple anvender for løse de opgaver der stilles, kan kommandoen infolevel benyttes, hvor nul, som er standard, angiver det laveste niveau og fem, det højeste. Til demonstration af dette bruges differentialligningen fra eks. 3

> infolevel[all] := 5;

> L3:=dsolve(DL3);

Methods for first order ODEs:

Trying to isolate the derivative dy/dx...

Successful isolation of dy/dx

--- Trying classification methods ---

trying a quadrature

trying 1st order linear

trying Bernoulli

combine:   combining with respect to   power

combine:   combining with respect to   power

combine:   combining with respect to   power

<- Bernoulli successful

combine:   combining with respect to   power

combine:   combining with respect to   power

combine:   combining with respect to   power

combine:   combining with respect to   power

evala/Indep:   testing independence of RootOfs

evala/Indep:   number of RootOfs   1

evala/Indep:   number of RootOfs   1

evala/Gcd/doit:   entering Gcd at time   411.998

evala/Gcd/doit:   exiting Gcd at time   412.000

evala/Gcd/doit:   entering Gcd at time   412.000

evala/Gcd/doit:   exiting Gcd at time   412.000

factor/polynom:   polynomial factorization: number of terms   3

evala/Factors:   starting factorization at time   412.004

evala/Factors:   starting factorization at time   412.004

factor/polynom:   polynomial factorization: number of terms   3

evala/Factors:   finishing factorization at time   412.006

evala/Factors:   number of factors   1

evala/Factors:   finishing factorization at time   412.007

evala/Factors:   number of factors   1

evala/Reduce/ff/urad:   Reducing radicals   [RootOf(3*_Z^2*x+x^3-3*_C1,label = _L7)]   at time   412.011

factor/polynom:   polynomial factorization: number of terms   3

factor/polynom:   polynomial factorization: number of terms   2

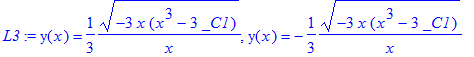
> L3:=bernoullisol( DL3, y(x));

trying Bernoulli

combine:   combining with respect to   power

combine:   combining with respect to   power

combine:   combining with respect to   power

<- Bernoulli successful

combine:   combining with respect to   power

combine:   combining with respect to   power

combine:   combining with respect to   power

combine:   combining with respect to   power

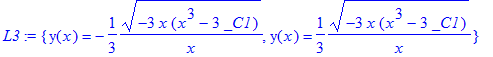
Som det fremgår af mellemregningerne, udfører Maple færre operationer når typen af differentialligningen er givet.

Infolevel skal nulstilles for at undgå disse mellemregninger.

> infolevel[all] := 0:

Ligesom bernoullisol , findes der lignende kommandoer til mange andre typer differentialligninger . Fordele ved, at angive typen er: 1) at Maple i visse tilfælde kun kan finde løsningen hvis typen er angivet, 2) at Maple hurtigere kan finde resultatet. I Maple 5 var følgende differentialligning et godt eksempel herpå, den blev nemlig kun løst delvist med kommandoen dsolve . For at få løst differentialligningen skulle man benytte kommandoen exactsol. I Maple 7 er der ikke dette problem, og differentialligningen løses på normal vis, vha. kommandoen dsolve.

Eks. 6: 1. orden, 1. grad, eksakt. Løs differentialligningen

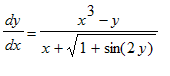
> DL6:=diff(y(x),x)=(x^3-y(x))/(x+sqrt(1+sin(2*y(x))));

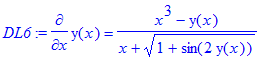
> dsolve(DL6);

Alle problemer er dog ikke løst, som det ses herunder kan odeadvisor ikke bruges, og man er nød til at afbryde beregningen ved at trykke på "stopknappen"

NB: problemet kan være løst i en opdateret, eller nyere version af Maple.

> #odeadvisor(DL6);

Desværre kan odeadvisor ikke klassificere differentialligningen. Der kan også søges hjælp på følgende måde:

> odeadvisor(DL6,[exact],help);

Desværre er der ingen mulighed for at få hjælp om differentialligningen

Sidste mulighed for at få klassificeret differentialligningen, er ved at benytte infolevel med den pågældende kommando som argument, her dsolve :

> infolevel[dsolve] := 5;

> L6:=dsolve(DL6);

Methods for first order ODEs:

Trying to isolate the derivative dy/dx...

Successful isolation of dy/dx

--- Trying classification methods ---

trying a quadrature

trying 1st order linear

trying Bernoulli

trying separable

trying inverse linear

trying homogeneous types:

trying Chini

differential order: 1; looking for linear symmetries

trying exact

<- exact successful

Hvis man læser mellemregningerne, ser man at Maple forsøger med forskellige løsningsmetoder, der forsøges bl.a. med Bernoulli og Chini. Længere nede i mellemregningerne forsøges der med den eksakte løsningsmetode, og i sidste linie står der exact successful, dette betyder at Maple har kategoriseret differentialligningen som værende Eksakt.

Tip: for at få hjælp om en kommando, tast ? foran.

Tip: # betyder, at det efterfølgende ikke betragtes som en kommando, og derfor ikke eksekveres.

> infolevel[dsolve] := 0: # Infolevel nulstilles ;-)

> test['L6'] = odetest(L6, DL6);

Eks. 9: 1. orden, lineær. Løs differentialligningen

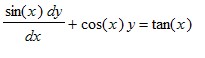
> DL9:=sin(x)*diff(y(x),x)+cos(x)*y(x)=tan(x);

Der findes en række plotkommandoer, som f.eks. dfieldplot der fremstiller et fasefelt for en given differentialligning . Ønskes der både et fasefelt samt løsningskurver for forskellige begyndelsesbetingelser, skal kommandoen phaseportrait anvendes. Men når nu pakken DEtools er åbnet, kan man lige så godt benytte den der i indbygget kommando DEplot som fremstiller fasefelter med eller uden begyndelsesbetingelser.

Tip: Der findes en masse muligheder hvorved man kan gøre sine plots lækre at se på, man kan bl.a. tilføje en overskrift ved at skrive title = " diagramtitel ", se følgende plot eller hjælpesider om plots.

> DEplot(DL9,y(x),x=-2..2,y=-2..2, color=blue, arrows=MEDIUM, title="Faseplot af DL9 uden begyndelsesbetingelser");

> odeadvisor(DL9);

> L9:=dsolve(DL9);

> test['L9']=odetest(L9,DL9);

Eks. 11: Bernoulli. Løs differentialligningen

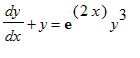
> DL11:=diff(y(x),x)+y(x)=exp(2*x)*y(x)^3;

I nedenstående plot er følgende underkommandoer benyttet: arrows angiver filetype, color / colour angiver pilefarve, stepsize angiver antal støttepunkter i linierne, linecolor angiver liniefarven, title angiver diagramtitel.

> DEplot(DL11,y(x),x=-1..1,[[y(0)=-2],[y(0)=-1],[y(0)=-0.5],[y(0)=0.5],[y(0)=1],[y(0)=2]],y=-2.5..2.5,arrows=medium,color=blue,stepsize=.05,linecolor=[red,blue,green,pink,aquamarine,khaki],title="Faseplot af DL11 med begyndelsesbetingelser");

Ja der findes en masse dejlige farver, man kan endda definere sine egne i f.eks. RGB format. Af en eller anden grund kan legend ikke benyttes i kommandoen phaseportrait som den kan i den almindelige plotkommando plot . Dog kan man højreklikke (PC) på ens plot, og vælge legend > show legend , derudover kan man også rette i linieforklaringerne ved at trykke legend > edit legend. Ulempen ved at tilføje linieforklaringer på denne måde er, at næste gang ens mapledokument eksekveres, vises linieforklaringerne ikke, og man skal derfor starte forfra med førnævnte metode.

Man kan også angive begyndelsesbetingelserne som er funktion

> DEplot(DL11, y(x), x=-1..1, [[y(0)=k/10]$k=-15..15], y=-2.5..2.5, color=blue, stepsize=.05, linecolor=red, arrows=medium, stepsize=.01);

Tilbage til løsningen af DL11:

> odeadvisor(DL11);

> L11:=dsolve(DL11);

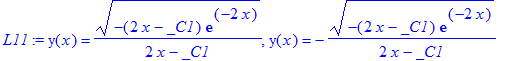
> test['L11'] = map(odetest,[L11],DL11);

For at differentiere et udtryk flere gange tilføjes $n til den variable, der differentieres med hensyn til, idet n angiver den n'te afledede. I tidligere versioner af Maple skrives variablen blåt det antal gange, som et udtryk skal differentieres. For at udskrive det uløste differentiale, skrives Diff (med stort d.)

> {Diff(cos(x),x,x)=Diff(cos(x),x$2)}={diff(cos(x),x,x)=diff(cos(x),x$2)};

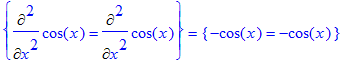
Eks. 12: 2. orden. Løs differentialligningen

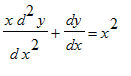
> DL12:=x*diff(y(x),x$2)+diff(y(x),x)=x^2;

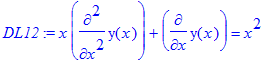
> odeadvisor(DL12);

> L12:=dsolve(DL12);

> test['L12']=odetest(L12,DL12);

Eks. 25b: 2. orden, inhomogen, konstante koefficienter. Løs differentialligningen

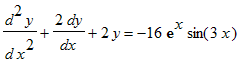
> DL25b:=diff(y(x),x$2)+2*diff(y(x),x)+2*y(x)=-16*exp(x)*sin(3*x);

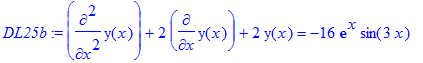
> odeadvisor(DL25b);

> L25b:=dsolve(DL25b);

> test['L25b']=odetest(L25b,DL25b);

Eks. 30: Lineære, 2. orden, inhomogen, variable koefficienter. Løs differentialligningen

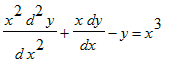
> DL30:=x^2*diff(y(x),x$2)+x*diff(y(x),x)-y(x)=x^3;

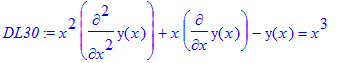
> odeadvisor(DL30);

> L30:=dsolve(DL30);

> test['L30']=odetest(L30,DL30);

Eks. 31: n'te orden, konst. koeff. Løs differentialligningen

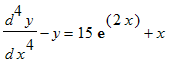
> DL31:=diff(y(x),x$4)-y(x)=15*exp(2*x)+x;

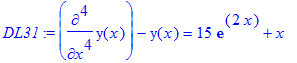
Når der plottes differentialligninger af anden eller højere orden med begyndelsesbetingelser, kan betingelserne angives med differentialoperatoren D :

> DEplot(DL31,y(x),x=-2.5..2.5,[[y(0)=1/2,D(y)(0)=0,(D@@2)(y)(0)=-4,(D@@3)(y)(0)=-1]],y=-2.5..2.5,stepsize=.05,linecolour=black,title="Faseplot af DL31 med begyndelsesbetingelser");

> odeadvisor(DL31);

> L31:=dsolve(DL31);

> test['L31']=odetest(L31,DL31);

Vi kan finde funktionsforskriften for ovenstående graf ved at løse L31 med de samme begyndelsesbetingelser som før. Som det ses, kan det igen gøres med differentialoperatoren D.

> L31:=dsolve({DL31,y(0)=1/2,D(y)(0)=0,(D@@2)(y)(0)=-4,(D@@3)(y)(0)=-1},y(x));

Et almindeligt plot af ovenstående funktion skulle så gerne se ud som DEplottet af DL31 .

> plot(rhs(L31),x=-2.5..2.5 ,y=-2.5..2.5);

differentialoperatoren D kan faktisk også bruges ved selve opskrivningen af en differentialligning på følgende måde.

> DL31:=(D@@4)(y)(x)-y(x)=15*exp(2*x)+x;

> L31:=dsolve(DL31,y(x));

Eks. 34: Sammenhørende differentialligninger.

Find det fuldstændige integral til de to sammenhørende differentialligninger 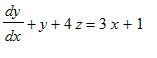og

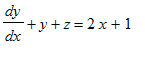
Systemer af differentialligninger indtastes på listeform omgivet af "tuborg"- parenteser og adskilt af komma.

> DLsys34 := {diff(y(x),x)+y(x)+4*z(x) = 3*x+1, diff(z(x),x)+y(x)+z(x) = 2*x+1};

Ved plot af differentialligningssystemer skal man angive "scenen" dvs. i hvilket plan man ønsker at betragte funktionerne projiceret i.

> DEplot(DLsys34, {y(x), z(x)}, x=-2..4, [[y(0)=-1, z(0)=-1], [y(0)=0, z(0)=0], [y(0)=1, z(0)=1]], stepsize=.05, scene=[z(x), y(x)], y=-1..2, linecolour=black);

Systemet kan også vises i 3D

Tip: hold musen over 3d-plottet, tryk og hold nede, og træk for at se plottet fra forskellige vinkler.

> DEplot3d(DLsys34, {y(x), z(x)}, x=-2..4, [[y(0)=-1, z(0)=-1], [y(0)=0, z(0)=0], [y(0)=1, z(0)=1]], y=-1..2, z=-1..4, scene=[x, z(x), y(x)], linecolour=black, axes=normal);

Man ikke få oplysninger om et differentialligningssystem vha. odeadvisor idet det jo består af to eller flere differentialligninger , dog kan man dele systemet op og kalde odeadvisor for hver enkel ligning.

Ved løsningen af systemet skal der til dsolve angives, hvilke funktioner der løses m.h.t. Disse funktioner angives på listeform.

> Lsys34:=dsolve(DLsys34, {y(x), z(x)});

> test['Lsys34']=odetest(Lsys34, DLsys34);

Partielle differentialligninger.

Når der skal udføres beregninger af partielle differentialligninger, skal pakken PDEtools kaldes.

> with(PDEtools);

Eks. 2. Find den fuldstændige løsning til differentialligningen

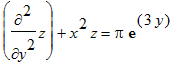
> PDL2:=diff(z(x,y),y$2)+x^2*z(x,y)=Pi*exp(3*y);

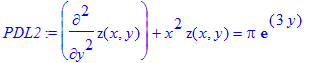
Til løsning af partielle differentialligninger benyttes kommandoen pdsolve.

> PL2:=pdsolve(PDL2);

Hvor _ F1 og _F2 er arbitrære funktioner af x .

Lige som det var tilfældet med almindelige differentialligninger, er det ved partielle differentialligninger også vigtigt at teste resultatet. Resultatet kontrolleres med kommandoen pdetest. V ises et 0 (nul) er resultatet korrekt.

> test['PL2']=pdetest(PL2,PDL2);

Eksempler på anvendelse af differentialligninger (svingningsteori).

> restart:with(DEtools):

, =

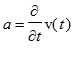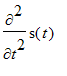
I eksemplerne betragtes et system bestående af et legeme med massen ophængt i en masseløs fjeder uden indre dæmpning med fjederkonstanten . s angiver strækningen og t angiver tiden .

Systemet startes til tiden uden begyndelseshastighed fra , hvilket giver anledning til følgende begyndelsesbetingelser: og

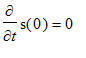
Eks. Frie udæmpede svingninger.

> DL1:=m*diff(s(t),t$2)+k*s(t)=0;

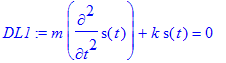
> odeadvisor(DL1);

> L1:=dsolve({DL1, s(0)=(1), D(s)(0)=0},s(t));

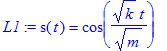
> test['L1']=odetest(L1,DL1);

Her tildeles s løsningsudtrykket fra DL1

> s:=unapply(rhs(L1),t);

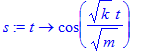
For at vise funktionen grafisk, skal konstanterne defineres:

> m:=10;k:=100;

og dermed kommer funktionen til at se således ud:

> s(t);

> plot(s(t),t=0..10,thickness=2,title="fri udæmpet svingning");

Nu kan det vises, at Maple har nogle fantastiske plot-muligheder. Følgende eksempel er rimeligt simpelt i forhold til hvad der ellers kan udføres.

For at udføre eksemplet, skal der kaldes nogle plotkommandopakker.

> with(plots):with(plottools):

Warning, the name changecoords has been redefined

Warning, the names arrow and translate have been redefined

Herunder er opstillet en funktion der kan animere svingningerne i et masse- fjedersystem der svinger efter en given funktionsforskrift.

> animation:=proc(funktion,sek) local funk: funk:=unapply(funktion,t); display(seq(translate(rectangle([-0.25,0], [0.25,0.5],color=red),funk(t/10),0),t=0..sek*10), scaling= constrained, view=[-2..2,0..1], insequence=true); end :

Funktionen er opstillet således at man bare skal taste animation( funktion,sekunder ) hvor funktionen indtastes på funktion 's pladsen og antal af sekunder animationen ønskes vist i, indtastes på sekunder 's plads, nemmere kan det ikke være!. Der kan være afvigelser i tiden fra computer til computer, forstået på den måde, at animationen måske ikke varer præcis 10 sekunder.

Vi prøver nu at indtaste ovenstående funktion for s(t) ind med et tidsforløb på 10 sekunder. Som det ses, starter massen ved +1 og det var jo netop værdien for funktionens begyndelsesbetingelse!.

For at se animationen: klik på figuren og tryk play .

> animation(s(t),10);

Eks. Dæmpede svingninger.

Legemet fra ovenstående system kunne f.eks. være nedsænket i en væske. Derved ville systemet have en dæmpning, afhængig af den pågældende væskes viskositet samt legemets fysiske udformning. Derfor tilføjer vi et ekstra led for dæmpningen, med dæmpningskonstanten c som faktor.

Først skal s(t) nulstilles.

> s:='s';

s kan tildeles med alle de variable der indgår i differentialligningen DL2 , således kan man indsætte talværdier på de samme pladser for derved, at kunne illustrere evt. ændringer i systemet. For at kunne gøre det, skal m og k nulstilles:

> m:='m':k:='k':

> DL2:=m*diff(s(t),t$2)+c*diff(s(t),t)+k*s(t)=0;

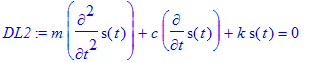
> odeadvisor(DL2);

> L2:=dsolve({DL2, s(0)=(1), D(s)(0)=0},s(t));

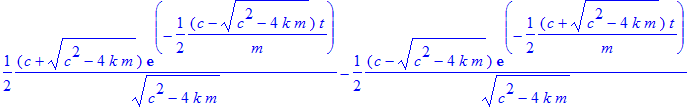
> test['L2']=odetest(L2,DL2);

Her tildeles s løsningsudtrykket for differentialligningen DL2 , men denne gang også med m, c og k som variable.

> s:=unapply(rhs(L2),t,m,c,k);

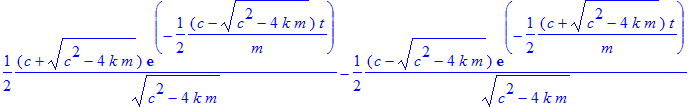
Først vises plottet med de tidligere angivet værdier for konstanterne m og k , og med en værdi af dæmpningskonstanten c på 10.

> plot(s(t,10,10,100),t=0..10,thickness=2,title="fri dæmpet svingning k = 100");

Herefter kan det illustreres hvilken betydning en ændring af systemets fjederkonstant ville have på svingningerne. Fjederkonstanten ændres fra 100 til 10 ved blåt at skrive 10 på k 's plads

> plot(s(t,10,10,10),t=0..10,thickness=2,title="fri dæmpet svingning k = 10");

Ydermere er det muligt at fremstille et tredimensionalt plot hvis bare vi undlader, at indsætte tal på de pladser i funktionen s , som vi ønsker at holde variable. Det kunne f.eks. være interessant, at se hvilken indflydelse, ændringer af dæmpningskonstanten c ville medføre. Vi vælger derfor at holde t og c variable.

> plot3d(s(t,10,c,100),t=0..10,c=0..10, axes= framed);

Her er det tydeligt illustreret, at når dæmpningskonstanten c øges, uddør svingningerne hurtigere (naturligvis).

Vi kan også prøve at animere funktionen :-)

> animation(s(t,10,10,100),10);

Eks. Tvungen dæmpet svingning

Hvis legemet i ovenstående system påvirkes af en ydre, harmonisk virkende kraft, vil legemet udføre nogle svingninger, der dels afhænger af perioden og dels afhænger af amplituden, hvormed den ydre kraft virker.

> s:='s':

> DL3:=m*diff(s(t),t$2)+c*diff(s(t),t)+k*s(t)=f[0]*cos(omega*t);

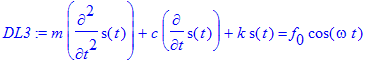
> odeadvisor(DL3);

> dsolve(DL3);

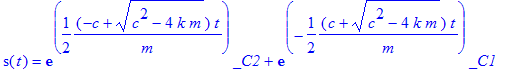
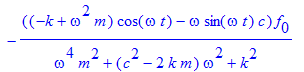
Af hensyn til visualiseringen af systemets svingninger er det en fordel, at opdele differentialligningens løsning i den homogene del og den partikulære del.

Den homogene del af differentialligningen:

> DL3[h]:=lhs(DL3)=0;

og dens løsning:

> s[h]:=unapply(rhs(dsolve({DL3[h], s(0)=(1), D(s)(0)=0}, s(t))), t,m,c,k);

Den partikulære del af differentialligningen:

> s[p]:=unapply(f[0]*((k-omega^2*m)*cos(omega*t)+omega*sin(omega*t)*c)/(omega^4*m^2+(c^2-2*k*m)*omega^2+k^2),t,m,c,k,f[0],omega);

Den fuldstændige løsning af differentialligningen er

> s[f]:=unapply(s[h](t,m,c,k)+s[p](t,m,c,k,f[0],omega),t,m,c,k,f[0],omega);

Inden de respektive funktioner kan plottes, skal resten af konstanterne defineres.

> #f[0]:=20;

> plot(s[h](t,10,10,100),t=0..10,s=-1..1,color=green, thickness=1,title="s[h](t) = systemets egensvingninger");

> plot(s[p](t,10,10,100,100,10),t=0..10,s=-1..1,color=blue,thickness=1,title="s[p](t) = den drivende kraftpåvirkning");

> plot(s[f](t,10,10,100,100,10),t=0..10,s=-1..1,color=red,thickness=1,title="tvungen dæmpet svingning omega=1");

Det fremgår af grafen, at den harmoniske kraftpåvirkning af systemet overtager efterhånden som systemets egensvingninger aftager.

De tre ovenstående grafer kan også vises i samme koordinatsystem.

Tip: tilføj linieforklaringer i almindelige plots med kommandoen legend, på følgende måde:

> plot([s[h](t,10,10,100),s[p](t,10,10,100,100,10),s[f](t,10,10,100,100,10)],t=0..10,s=-1..1,thickness=1,color=[green,blue,red],title="tre plots med linieforklaringer", legend=["s[h] (t)", "s[p] (t)", "s[f ] (t)"]);

Her er det ligeledes muligt at vise svingningerne vha. vores animationsfunktion. Ønsker man at ændre animationens afspilningshastighed, ganges en faktor på t

> animation(s[f](t,10,10,100,100,10),10);

Eks. dobbelt frit udæmpet svingningssystem.

> restart:with(DEtools):

Systemet består, set fra venstre, af en fjeder k1 , en masse m1 , en fjeder k2 , en masse m2 , og tilsidst igen en fjeder k3 , fjedrene er fastgjort ude ved enderne således, at de to masser kan svinge herimellem.

Alle konstanterne defineres

> m1:=10:m2:=10:k1:=20:k2:=20:k3:=20:

Differentialligningssystemet opstilles

> SvingSys := {m1*diff(s1(t), t$2)=-k1*s1(t)+k2*(s2(t)-s1(t)), m2*diff(s2(t), t$2)=-k2*(s2(t)-s1(t))-k3*s2(t)};

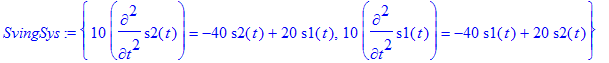
og løses idet, at massen m1 er forskudt længden 1 i positiv retning til tiden t = 0

> dsolve(SvingSys union {s1(0)=1, D(s1)(0)=0, s2(0)=0, D(s2)(0)=0},{s1(t),s2(t)});

og her er en fiks måde at tildele udtryk på, således at man efterfølgende bare skal skrive hhv. s1(t) og s2(t)

> assign(%);

> 's1(t)'=s1(t);'s2(t)'=s2(t);

løsningsfunktionerne plottes

> plot([s1(t),s2(t)],t=0..20,s=-1..1,color=[red,blue], legend=["m1", "m2"]);

Nu kan man lave en animation af systemet hvor 2 på den vandrette akse er m1 's nulpunkt og 4 er m2 's nulpunkt

> with(plots):with(plottools):

Warning, the name changecoords has been redefined

Warning, the names arrow and translate have been redefined

> animation:=proc(funktion1,funktion2,sek) local funk1, funk2, ma, mb, mab: funk1:=unapply(funktion1,t); funk2:=unapply(funktion2,t); ma:=t->translate(rectangle([0,0], [0.5,0.5],color=red),1.75+funk1(t),0); mb:=t->translate(rectangle([0,0], [0.5,0.5],color=blue),3.75+funk2(t),0); mab:=t->display([ma(t/10),mb(t/10)]); display(seq(mab(t),t=0..sek*10),scaling= constrained, view=[0..6,0..1], insequence=true); end :

Det ses at m1 starter på 3 hvilket svarer til en forskydning på 1 som jo netop var den aktuelle begyndelsesbetingelse.

> animation(s1(t),s2(t),20);